State-of-the-art relational data representation and processing are highly redundant. This project investigates the sources of this redundancy and proposes alternatives that avoid it.
For relational join processing, the culprit behind this redundancy is the Cartesian product lurking within every database join. By avoiding the listing (enumeration) of the output of these products, we can lower the space and computational costs for joins. See first this simple example and then the second more insightful example .
This redundancy can be avoided via factorisation
We developed three distinct lossless factorised representations for join queries and even the more general functional aggregate queries:
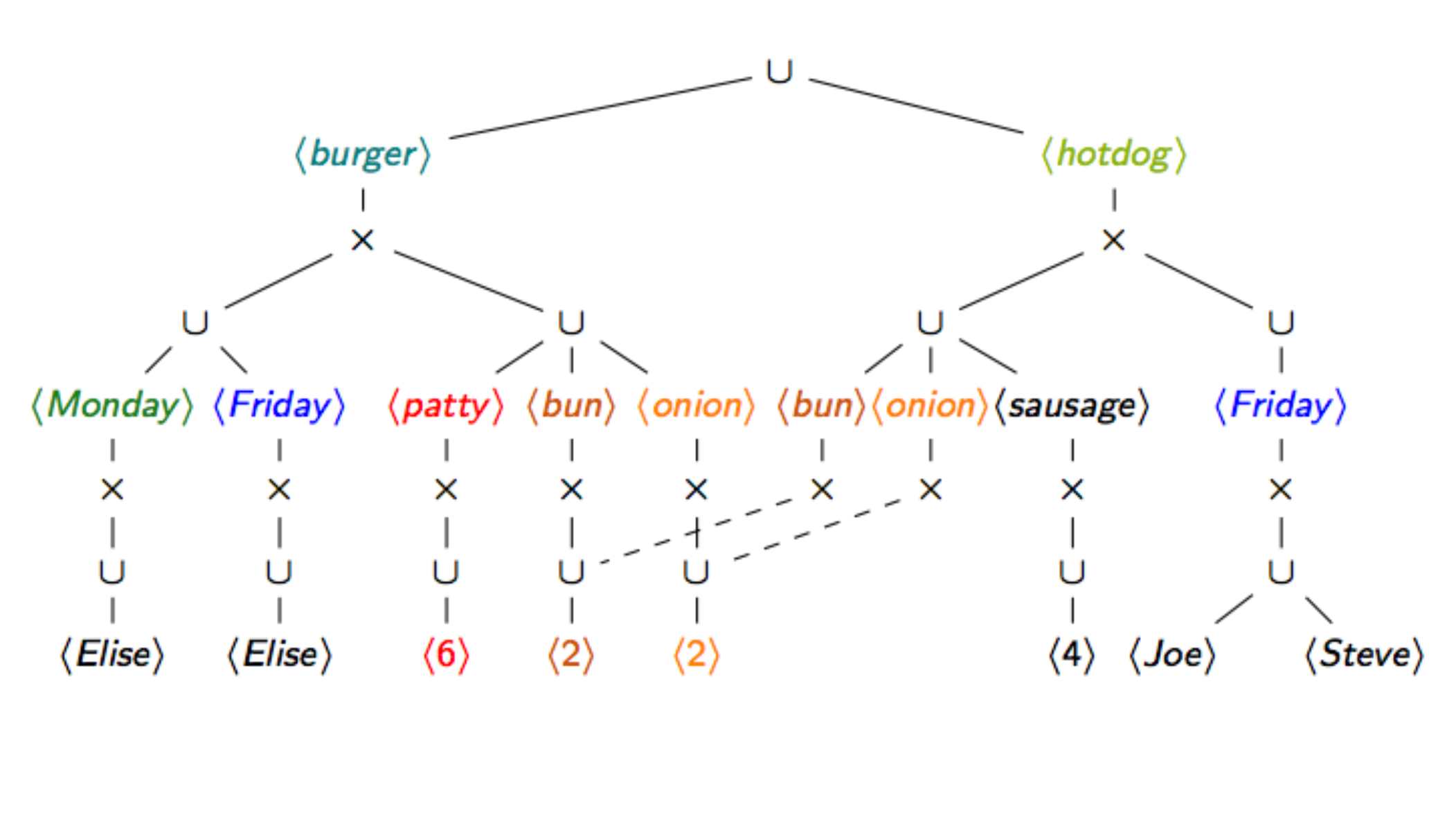
- The f-representations (see ICDT'12 paper ) are to the listing representation what nested formulas are to formulas in disjunctive normal form. They are relational algebra expressions with operators union and product over singleton relations (relations with one column and one row). They exploit the distributivity of the product over union to factor out common subexpressions.
- The d-representations (see TODS'15 article ) are f-representations with definitions: A recurring subexpression can be given a name and referenced several times by name instead of content. They correspond to circuits.
- The covers (see ICDT'18 paper ) of a query result is a minimal subset of this result from which we can losslessly reconstruct it entirely.
Compression by factorisation can also be applied to query provenance or lineage ( ICDT'12 and TAPP'11 papers).
Analytics can be computed directly over factorised data
The factorised representations of a join result allow for the enumeration of the result tuples with
constant delay, which
is as efficient as enumerating them from the listing representation of the result. This is a
prerequisite
for the computation of aggregates (and more complex analytics) in one pass over factorised data.
In case the materialisation of the factorised join result is not desirable, aggregates can be computed
on
the fly. In this case, the
trace
of the aggregate-join computation is that of the underlying factorisation and corresponds to (partially)
pushing aggregates past joins.
To explore more on: constant-delay enumeration and worst-case optimal join factorisation see the
TODS'15 article
; factorised join plans see the
VLDB'12
paper; aggregates over factorised joins see the
SIGMOD Record'16
and
VLDB'13
papers; machine learning over factorised joins see the
SIGMOD'16
and
PODS'18
papers.