Redundancy in Join Results

Consider the following database with three relations Orders (O), Dish (D), and Items (I).

The natural join of the three relations entails loads of redundancy, as shown below for a fragment of it. For instance, the values Elise and burger appear in all tuples in this fragment.

Getting Rid of Redundancy using Factorisation

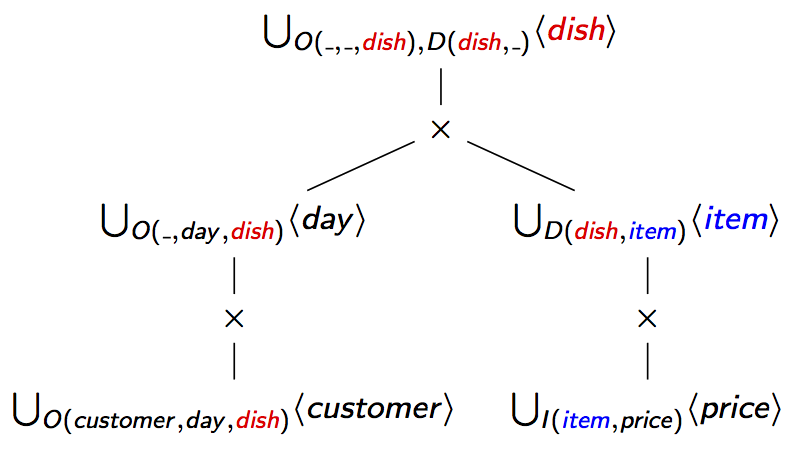
How can we get rid of this redundancy? Let us have a closer look at this result fragment through relational algebra glasses. This relation can be expressed in relational algebra using the operators union and Cartesian product over singleton relations (relations with one column and one row).

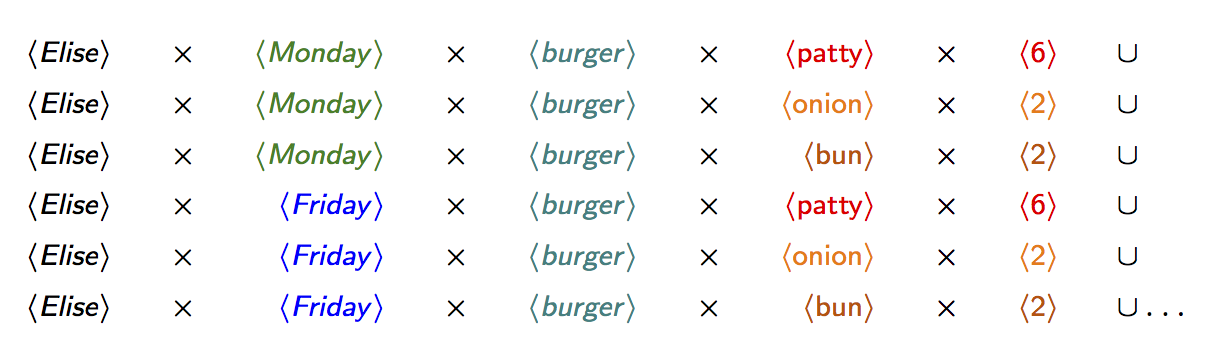
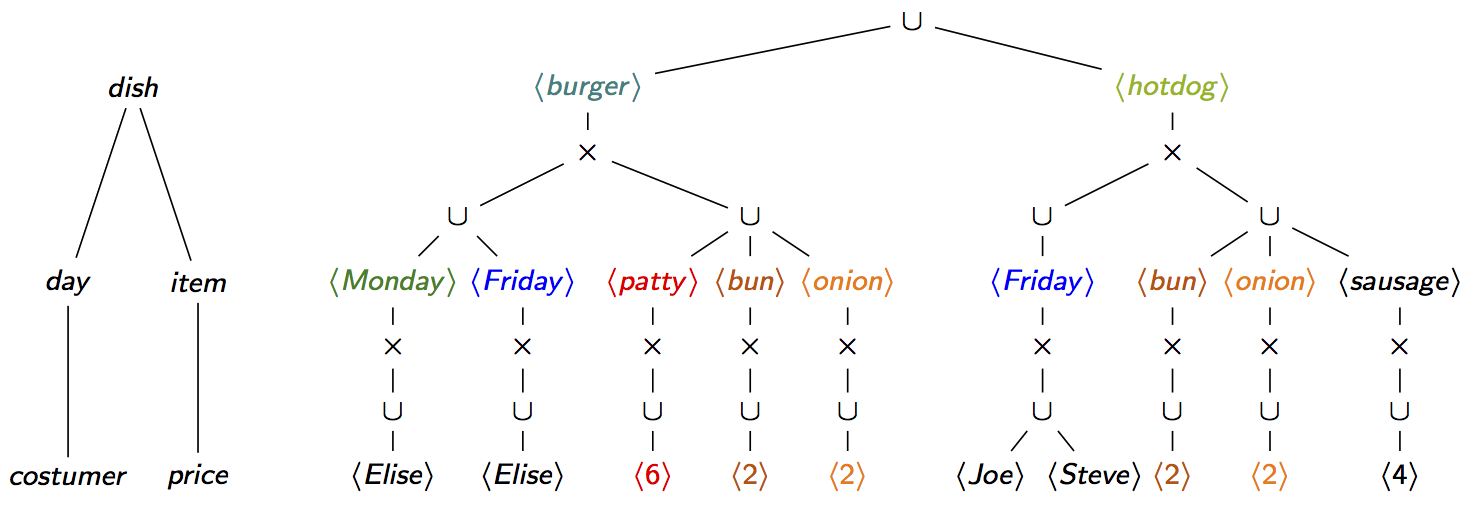
We can simplify this algebraic expression by using the distributivity of the product over union to factor out common subexpressions. One possible factorisation is given below (right). Its structure (left) is given by a partial order on the query variables, or variable order for short, which is sometimes called f-tree for factorisation tree; a more refined version is called d-tree.
The f-tree below means the following: We first enumerate the possible dishes. For each dish, we consider independently the list of days when the dish is ordered from the list of component items of the dish. Under each day, we enumerate the customers who ordered on that day the dish. Also, under each item, we have its price.

The above factorisation exploits some of the join dependencies, or equivalently the conditional independence, present in the join result: Given the dish variable, the variables day and customer on one hand and the variables item and price on the other hand are independent in the sense that values for the latter do not restrict the possible values for the former.
In f-trees, a variable is assumed to depend on all its ancestor variables. This simplification leads to factorisations that are trees: For each tuple of values of the ancestor variables, we list the possible valid values of the current variable. This assumption is not necessarily justified. For instance, price does not depend on dish given item. In general, a variable may only depend on a subset of its ancestors.
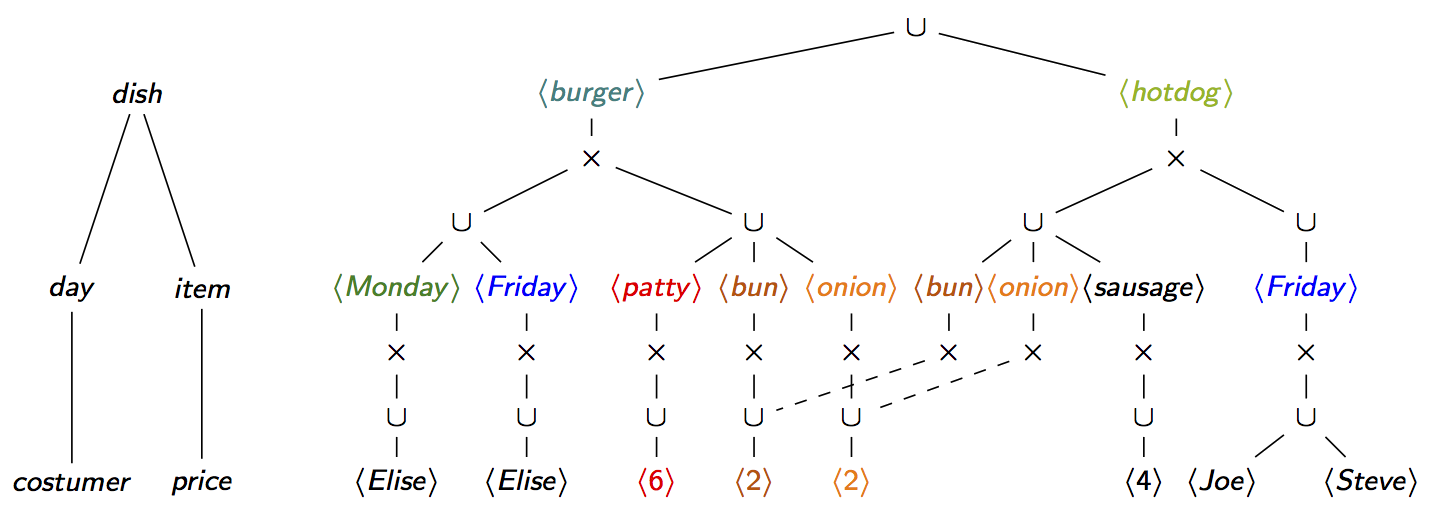
The d-trees, which are variable orders that refine f-trees, explicitly associate with each variable its dependency set that consists of those ancestor variables on which it depends or its descendants depend. The d-trees may lead to more compact factorisations, as depicted next.

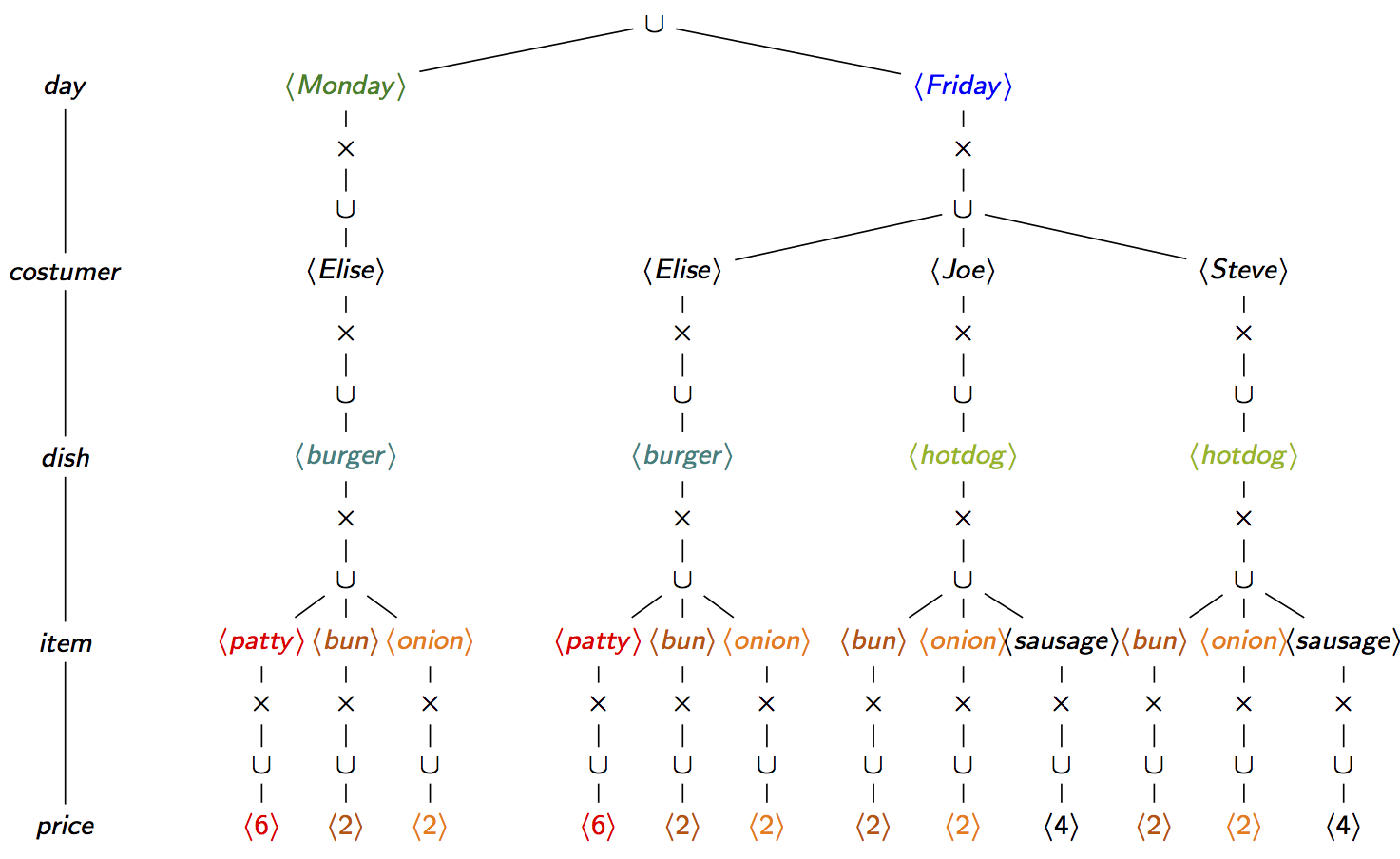
The above factorisations are not the only one possible for our join result. Indeed, different variable orders lead to different factorisations. The factorisation below is over an f-tree that is a path; in this case, the factorisation becomes a trie and does not exploit the join dependencies.

We can turn the previous path f-tree into a d-tree by noting the conditional independence between the query variables. The factorisation over this d-tree now becomes much more compact.

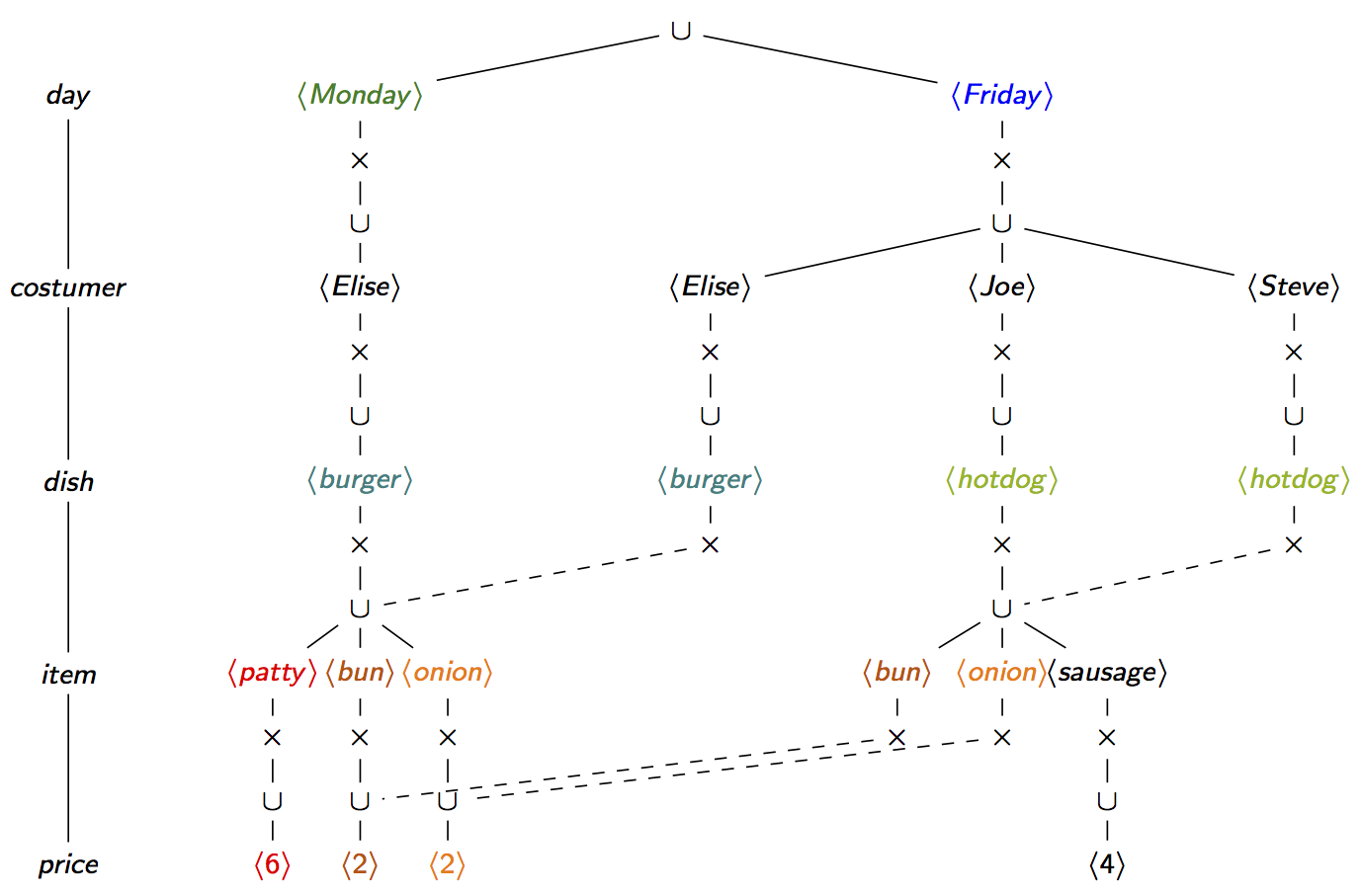
An important question is which d-trees lead to asymptotically smallest factorisations and hence of worst-case optimal size within the class of factorisations whose structure is given by f-trees and respectively d-trees. This question is answered in the ICDT'12 paper for f-trees and in the TODS'15 article for d-trees.

How To Compute Factorised Joins?

Given a variable order, we can compute the factorisation in worst-case optimal time. At each variable in the order, we compute the join of all relations on that variable: At dish, we intersect the relations Orders (O) and Dish (D) on dish; at day, we look up into Orders the days for a given dish and then at customer we look up into Orders the customers for the given day and dish. We proceed similarly on the right branch. These lookups and intersections can be done efficiently if the relations are sorted following a topological order of the variable order. To guarantee optimality, the intersection of several lists needs to take time linear in the size of the smallest list (modulo a log factor).

How To Compute Aggregates over Factorised Joins?

We now turn to a different question: How to evaluate aggregates over the previous factorised join? It turns out that common SQL aggregates, such as SUM, MIN, and MAX can be evaluated in one pass over factorisations.
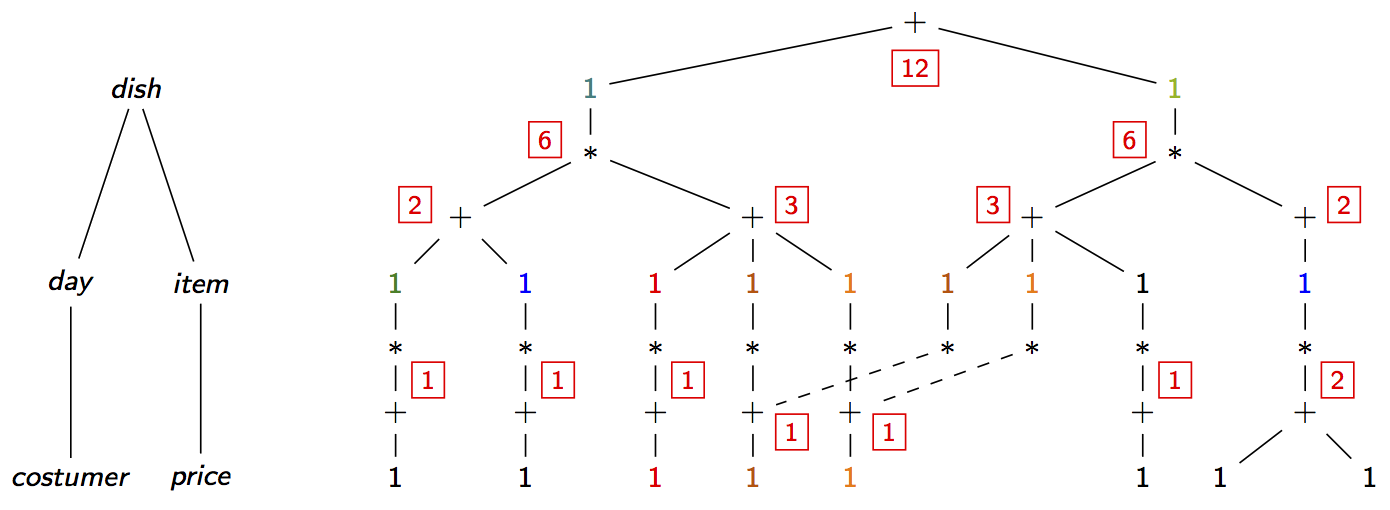
Consider the computation of the count aggregate COUNT(*) over our above factorisation whose structure is given by the d-tree with two branches. This aggregate computes the number of tuples in the join result. We do this in one bottom-up pass over the factorisation, where we interpret each singleton relation as value 1 and map each union and Cartesian product operator to arithmetic addition and respectively multiplication. As shown below, the factorisation saves computation time by avoiding counting the tuples and instead replacing a summation of the same number by multiplication.

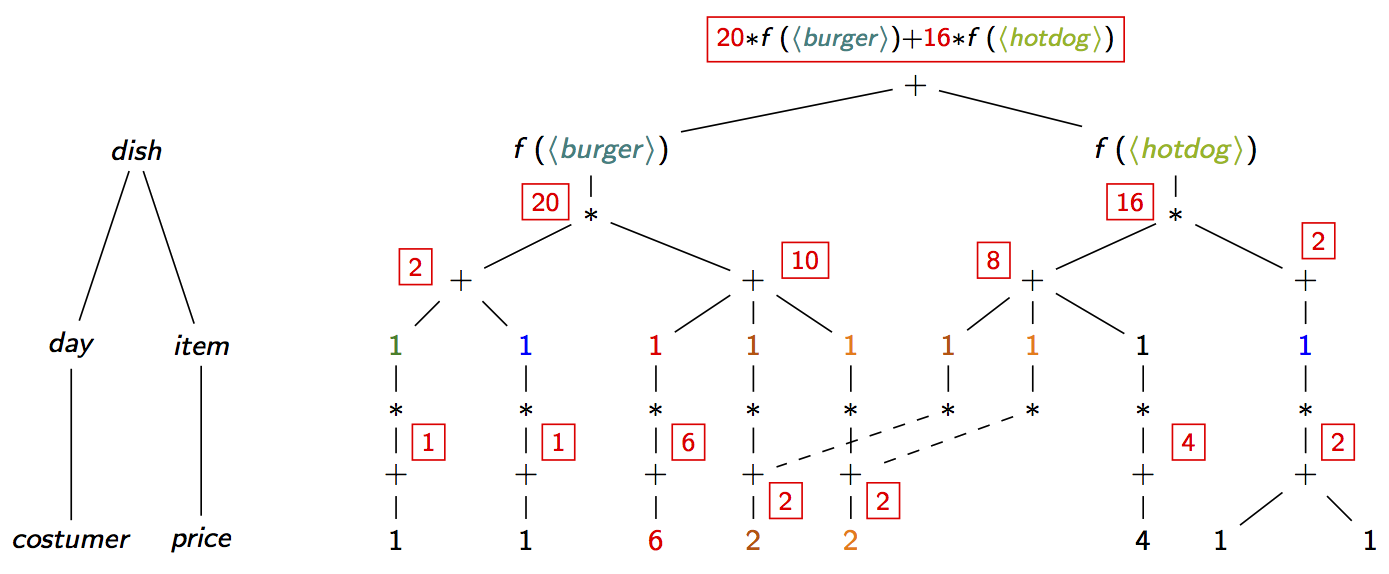
More complex aggregates are also possible. Below is the case of the aggregate SUM(dish * price): We map all values except for dish and price to 1, union and product to arithmetic addition and respectively multiplication. Since dish is not a numerical variable, we assume here there is a function $f$ that turns dish into reals.

The above aggregates have no GROUP-BY clauses (or free variables). We can compute them as exemplified above in one pass over factorisations with any structure. This is not the case however for aggregate with GROUP-BY clauses, whose computation is sensitive to the structure of the factorisation: In particular, as long as the GROUP-BY variables lie above the other variables in the variable order, the aggregates can be computed in one pass over the factorisation. Furthermore, the computation of ORDER-BY clauses is also sensitive to the structure of the factorisation: Like for GROUP-BY, the ORDER-BY variables need to lie above the other variables in the variable order. Moreover, the order of the ORDER-BY variables must match a topological order of the variable order.
More on this topic is available in the PVLDB'13 and the more recent SIGMOD Record'16 articles.