Motivation

Our aim is to build a database engine that provides scalable techniques to compute machine learning models over normalised databases. We show that the data-intensive computations of many machine learning models can be factorised and computed directly inside a database engine. Doing so can lead to orders-of-magnitude performance improvements over current state-of-the-art analytics systems. In addition, a host of machine learning models can be learned with the same low complexity guarantees as factorised query processing (see Principles of Factorised Databases for details).

Why in-database analytics?

For many practical scenarios, machine learning models are computed over several data sources that are stored in a database management system (DBMS). Machine learning algorithms, on the other hand, require as input a single design matrix, which means that the distinct data sources need to be joined into a single relation.

In a conventional technology stack, the join is computed in a DBMS and the join result is then exported into a specialised analytics system that computes the machine learning model. Computing the machine learning model directly in the DBMS has several non-trivial benefits over the conventional approach with specialized systems:

1. In-database analytics brings analytics closer to the data.
   Computing the machine learning model directly in an optimized DBMS implies that we can avoid the time-consuming import/export step between the specialised systems in a conventional technology stack.


2. In-database analytics can exploit the benefits of factorised join computation.
   As shown in the Principles of Factorised Databases project, listing representations of relational data are known to require a high degree of redundancy for data representation and computation, especially in the case of relations representing joins. This redundancy is not necessary for subsequent processing, such as learning regression or classification models, and we avoid such redundancy by computing machine learning algorithms over factorised joins instead. By doing so, we are able to show that the data-intensive computation of many machine learning models follows the low complexity guarantees of factorised query processing. In fact, computing the model over the factorised joins can take less time than computing the conventional listing representation of the join only!


3. In-database analytics can exploit relational structures in the underlying data.
   When computing a machine learning model inside a database engine, it is possible to exploit relational structures in the underlying data to compute machine learning models faster. For instance, we can exploit functional dependencies to decrease the dimensionality of a machine learning model, which leads to significant performance improvements (see our PODS'18 paper).

Our Approach to In-Database Analytics

The data-intensive computations of a large class of machine learning models can be rewritten into aggregates over joins and factorised. This class includes (among others) regression, principal component analysis, decision trees, random forests, naive bayes, Bayesian networks, k-nearest neighbors, and frequent itemset mining. Our experiments show that this rewriting can lead to performance improvements of several orders-of-magnitude over over systems like R, Python StatsModels, and MADlib, while maintaining the accuracy of these competitors (see our SIGMOD'16 paper for details).

The conventional technology stack compared to our approach to in-database analytics .

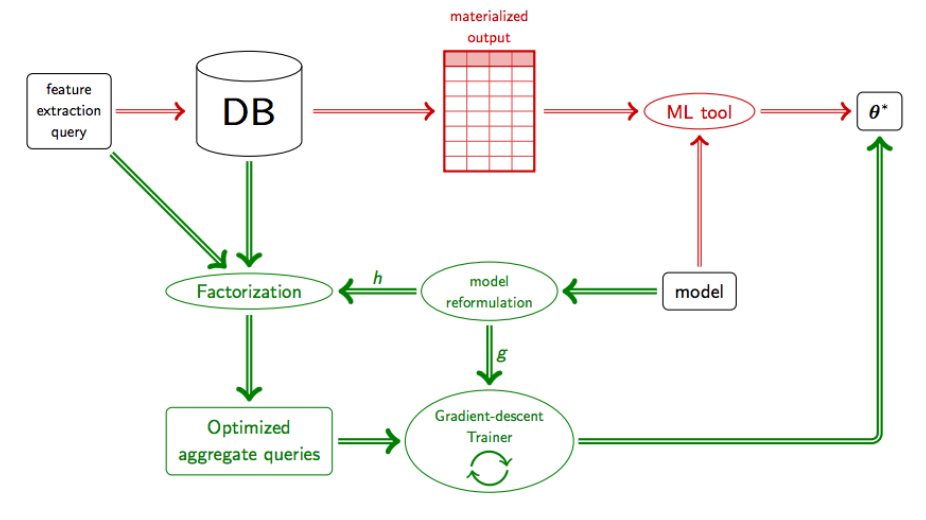
Example: Consider the above Figure, which gives a high-level overview of our approach to in-database anayltics.
In a conventional technology stack (the red part of the diagram), a feature extraction query is issued to the database engine which computes and materialises the output table. This table is then imported into a machine learning tool that learns and outputs the best model parameters $\mathbb{\theta^*}$.
In our in-database analytics framework (the green part), we rewrite the query and model formulation into highly optimized factorized aggregate queries. These queries capture the data-intensive part of the machine learning model, which is fed into an optimisation algorithm (gradient descent in this case) which computes $\mathbb{\theta^*}$, without ever having to go back to the original data tables.

The rewriting of the data-intensive computation into aggregates over joins has additional benefits:

1. We can efficiently capture categorical variables, without any an intermediate encoding of the input data. Typically, categorical variables are one-hot encoded, which leads to a significant blow-up of the input data. We avoid such intermediate encodings by treating categorical variables as group-by variables in our aggregate queries (see PODS'18 paper for details).
2. We can exploit functional dependencies to decrease the dimensionality of the model (see our PODS'18 paper for details).
3. Aggregates computed for a model can be re-used to compute models over any subset of the original features, which means we can efficiently explore the feature space for the best model (see VLDB'16 demo paper for details).
4. The aggregates that capture the data-intensive computations of the model are distributive, which means these computations can be easily parallelized and distributed (see SIGMOD'16 paper for details).