Take for instance the natural join of two relations $R(A,B)$ and $S(A,C)$ and assume both relations have the $A$-values $a_1,\ldots,a_n$ for some large value of $n$. Partition the columns $B$ and $C$ of the two relations so that there is one partition per $A$-value: $R_i = \pi_B \sigma_{A=a_i}(R)$ and $S_i = \pi_C \sigma_{A=a_i}(S)$, for each $i\in [n]$. The join result is the union of the Cartesian products of the corresponding partitions in the two relations: $R\Join S = \{(a_1)\} \times R_1 \times S_1 \cup\cdots\cup \{(a_n)\} \times R_n \times S_n$.

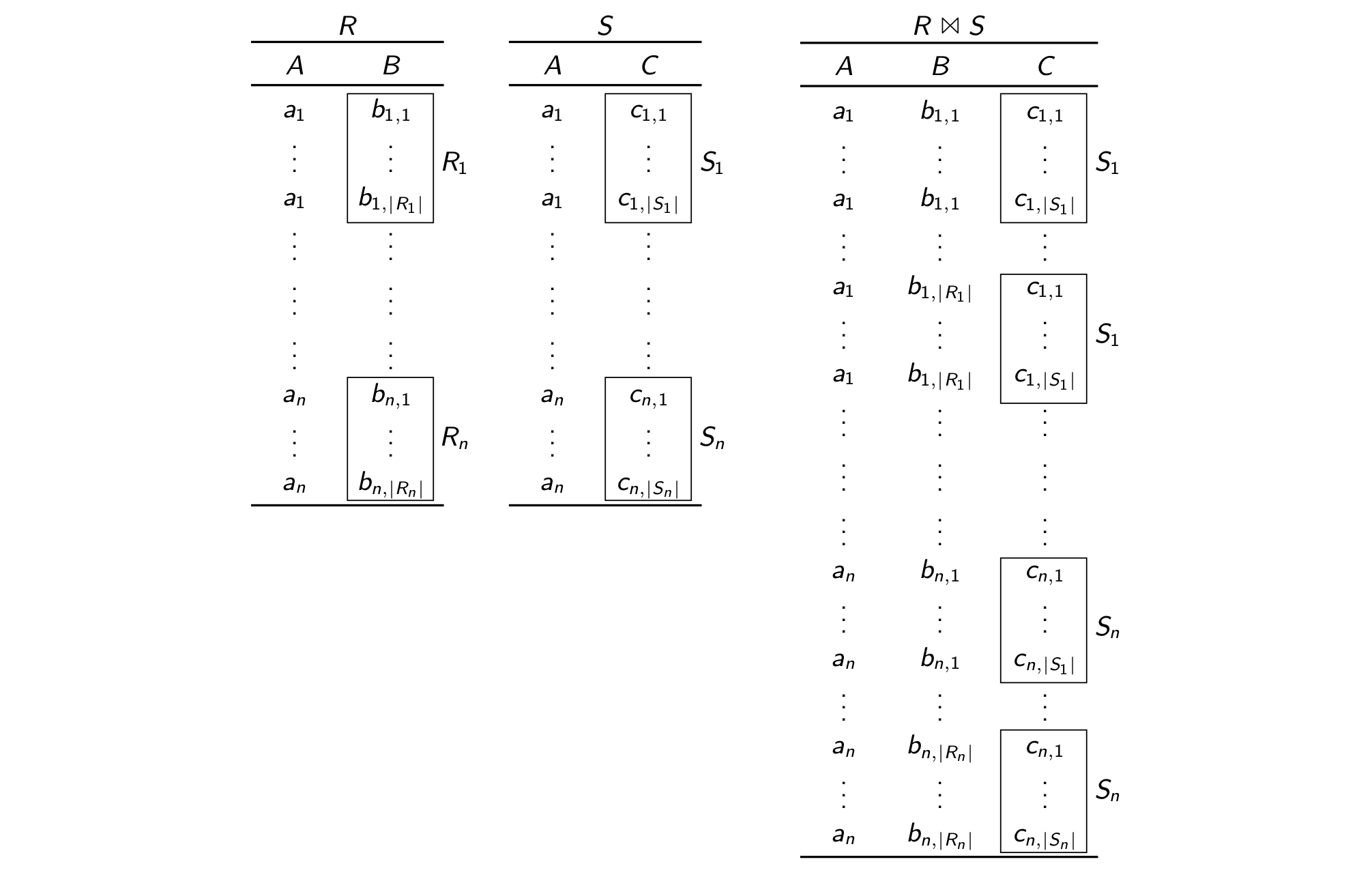
The listing (or row-oriented) representation of the join result, as depicted above, materialises the products. In general, the result may have quadratically many tuples and it takes quadratic time to compute. Our approach avoids the materialisation of these products and computes a representation that only takes linear size and time!
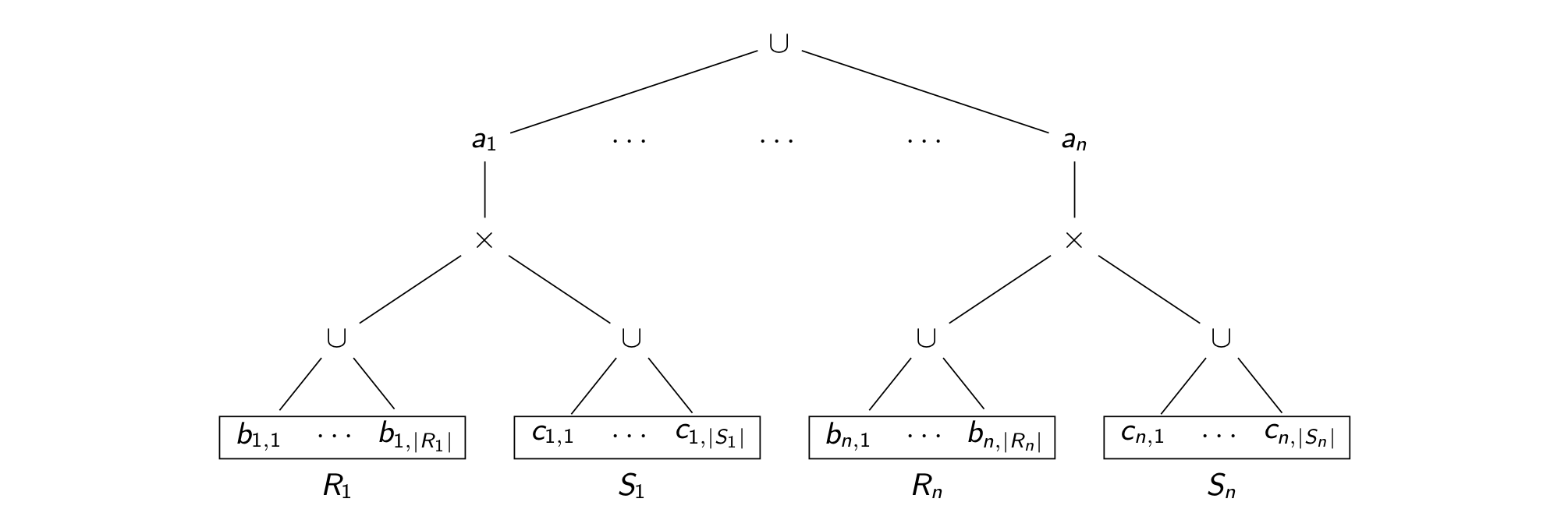
We can represent the join result as a tree that has a subtree for each $a_i$ with $i \in [n]$. The subtree of each $a_i$ lists all values in $R_i$ and $S_i$ at its leaves.

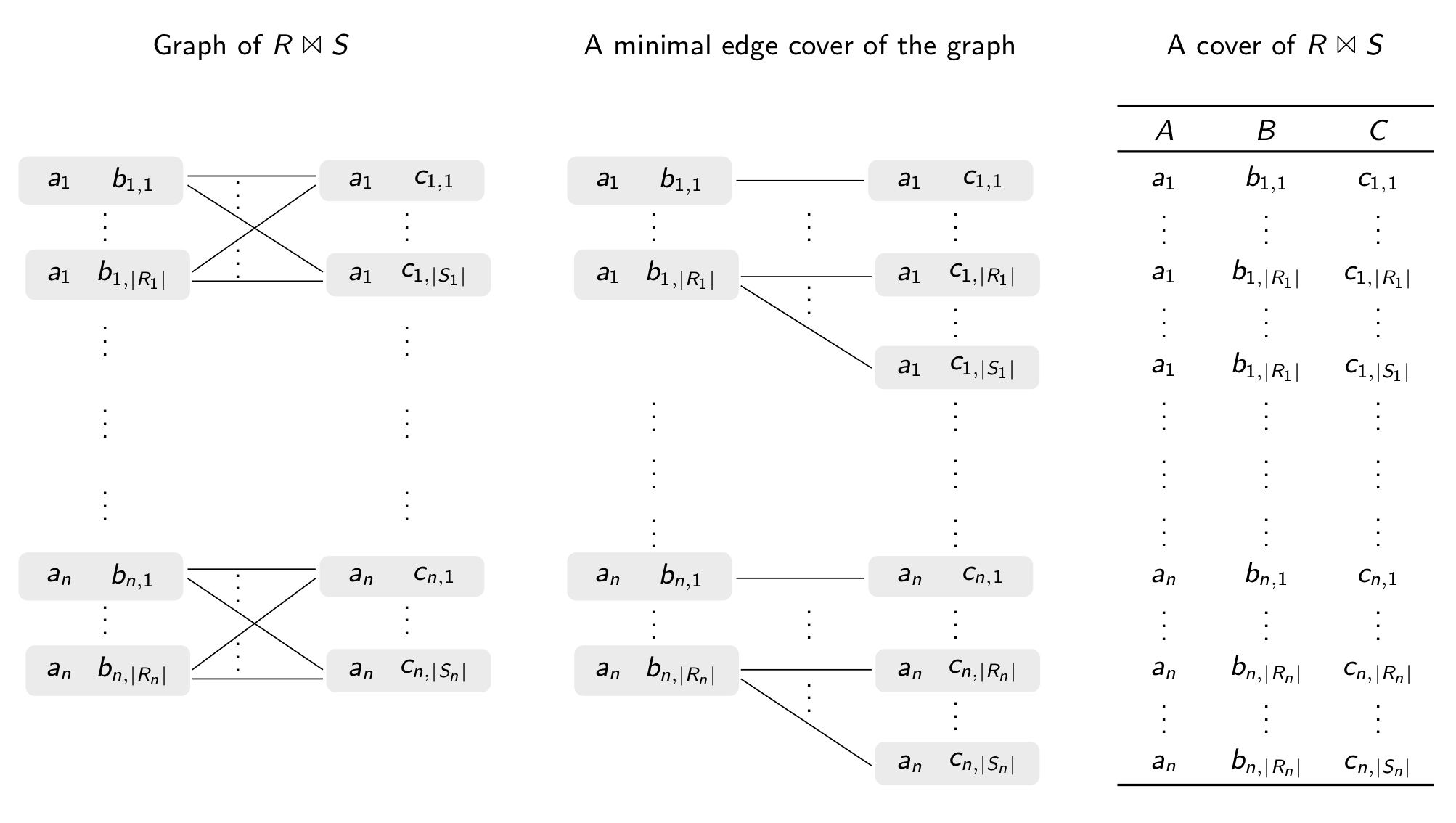
We can represent the join result also by only taking a linear-size subset of it that contains enough information to reconstruct the entire join result. Such a subset is called a cover of the join result. To construct a cover of $R \Join S$, we consider the bipartite graph of $R \Join S$. The nodes of this graph are the tuples in $R$ and $S$ and the edges connect joinable tuples. We take an arbitrary minimal edge cover of this graph. A cover of $R \Join S$ contains one tuple for each edge in such a minimal edge cover of the graph of $R \Join S$. The following picture shows a possible minimal edge cover of the graph of $R \Join S$ and the corresponding cover of $R \Join S$ in case $R_i \leq S_i$ for each $i \in [n]$.

These simple ideas can be applied to arbitrary join queries, albeit with a bit more effort. There exist queries and databases for which the sizes (and computation times) of our succinct representations of the query results are ${\cal O}(N)$, while the sizes (and computation times) of the listing representations are ${\cal O}(N^q)$, where $N$ is the size of the database and $q$ is the number of relations in the join query. This can lead in practice to many orders of magnitude improvement in performance for query processing in our approach versus the state-of-the-art!