This page depicts the landscapes of the static and dynamic query evaluation, and the relationship of our results (PODS'20) with prior results.

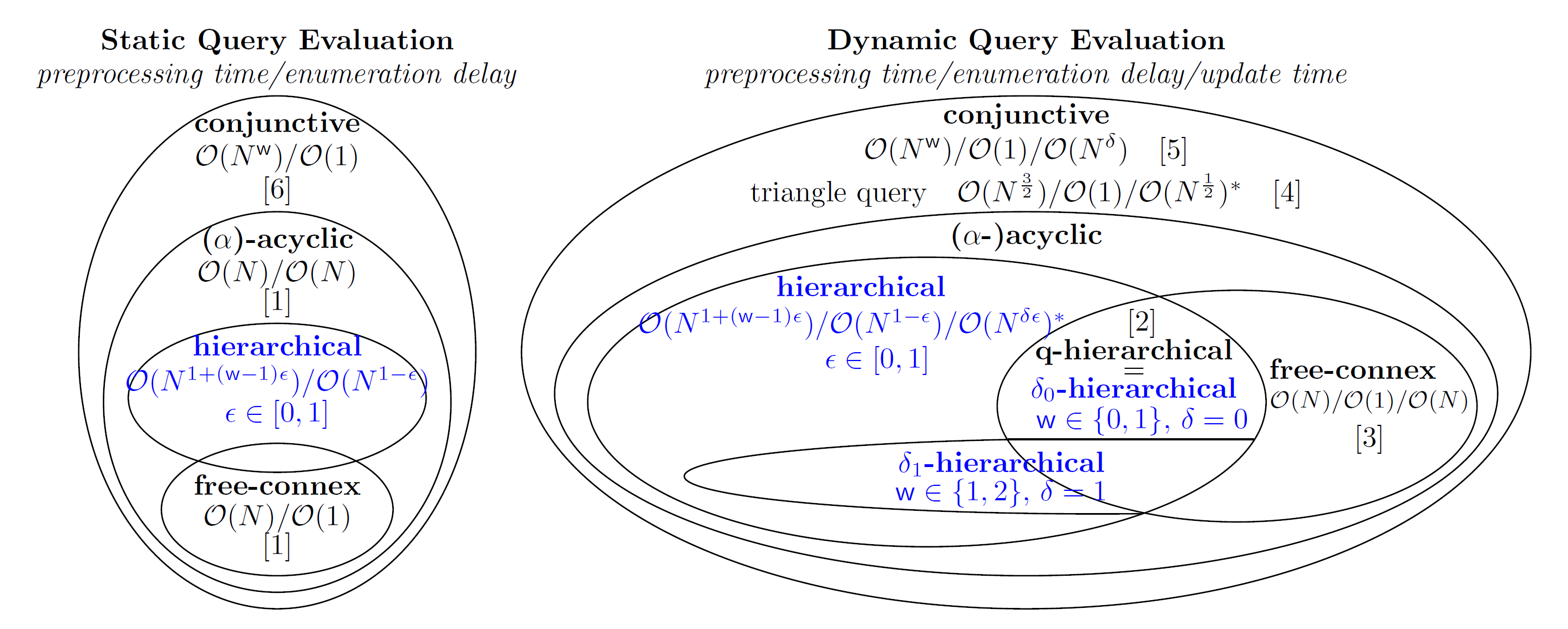
As shown in the left figure, our static result recovers the prior results for conjunctive queries [6] by setting $\epsilon = 1$ and $\alpha$-acyclic queries [1] by setting $\epsilon = 0$; For free-connex queries, $\mathsf{w} = 1$ and the preprocessing time remains O(N) regardless of $\epsilon$; we then recover the constant delay [1] by choosing $\epsilon$ = 1.

The right figure shows that by setting $\epsilon = 1$, our dynamic result recovers prior work on conjunctive [5], q-hierarchical [2] and free-connex [3] queries, where $\mathsf{w} = 1$ and $\delta \in \{0,1\}$ for free-connex queries and $\mathsf{w} = 1$ and $\delta = 0$ for q-hierarchical queries.

Reference

[1] Guillaume Bagan, Arnaud Durand, and Etienne Grandjean. On Acyclic Conjuntive Queries and Constant Delay Enumeration. In CSL, pages 208-222, 2007.

[2] Christoph Berkholz, Jens Keppeler, and Nicole Schweikardt. Answering Conjunctive Queries Under Updates. In PODS, pages 303-318, 2017.

[3] Muhammad Idris, Martin Ugarte, and Stijn Vansummeren. The Dynamic Yannakakis Algorithm: Compact and Effcient Query Processing Under Updates. In SIGMOD, pages 1259-1274, 2017.

[4] Ahmet Kara, Hung Q. Ngo, Milos Nikolic, Dan Olteanu, and Haozhe Zhang. Counting triangles under updates in worst-case optimal time. In ICDT, pages 4:1-4:18, 2019.

[5] Milos Nikolic and Dan Olteanu. Incremental View Maintenance with Triple Lock Factorization Benefits. In SIGMOD, pages 365-380, 2018.

[6] Dan Olteanu and Jakub Zavodny. Size Bounds for Factorised Representations of Query Results. ACM TODS, 40(1):2:1-2:44, 2015.